Какой подход используется в Python?

На интуитивном уровне многие считают, что деление нацело (оператор //) сводится к отбрасыванию дробной части. То есть из 2.4 получаем 2, а из -2.4 получаем -2. Это деление с округлением к нулю, и остаток считается соответствующим образом, то есть его знак совпадает со знаком делимого. Во многих языках, от Pascal до C#, используется именно этот подход.

Но создатель Python, Гвидо ван Россум, выбрал другой подход: результат целочисленного деления всегда округляется вниз. За использование деления с округлением вниз в информатике также выступал Дональд Кнут, известный математик и автор книги «Искусство программирования».

Соответственно, в Python -5 // 2 - это -3, а не -2. Знак остатка при этом совпадает со знаком делителя.

Почему именно деление с округлением вниз?

Всё дело в ситуациях, в которых на практике используются операторы // и %.

Например, представьте себе поле размером NxM пикселей. Оно разбито на блоки размером 4х4 точки каждый.

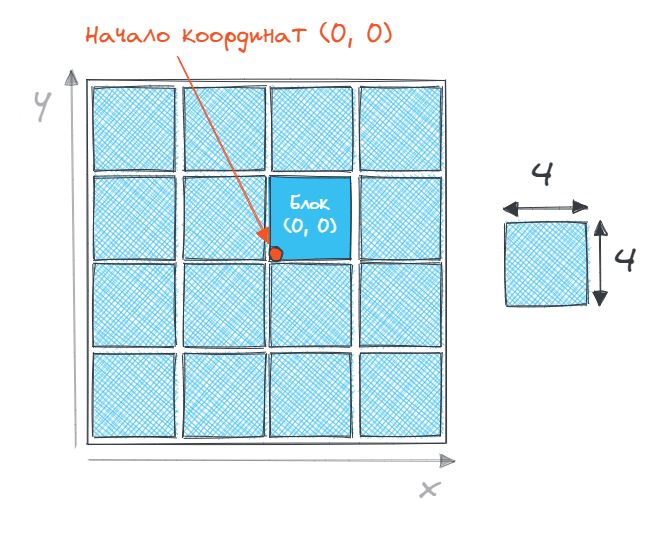
Будем работать со следующими сущностями:

1. Координаты конкретной точки на поле, например, (-38, 11);
2. Номер конкретного блока. Например, блок (0, 0) - это тот, в левом нижнем углу которого находится начало координат. Справа от него блок с позицией (1, 0), а сверху - (0, 1);
3. Координаты точки внутри блока. Если ширина блока - 4х4, то координаты точки внутри блока могут меняться от (0, 0) (нижний левый угол) до (3, 3) (верхний правый угол).

И теперь представим, что у нас есть координаты какой-то точки на поле, например, (-38, 11). Как узнать, в каком блоке находится эта точка и какую конкретно позицию внутри блока она занимает? Довольно легко, если в языке используется деление с округлением вниз:

Обратите внимание на то, что с отрицательными координатами всё работает абсолютно корректно. А если бы использовалось деление с округлением к нулю, то для координат (-6, -8) мы получили бы некорректные результаты:

Координаты: (-6, -8)
Позиция блока: (-1, -2)
Позиция пикселя в блоке: (2, 0)

Очевидно, что координата x: -6 никак не может находиться в блоке, имеющем позицию x: -1, потому что ширина блока - 4 пикселя.

Какой подход лучше?

Любой.

Цель статьи не в том, чтобы сказать, что в Python используется хороший или плохой подход. Споры на тему того, как нужно правильно делить, идут уже давно, и навряд ли завершатся в обозримом будущем. Гвидо ван Россум и Дональд Кнут считают, что в программировании удобнее использовать деление с округлением вниз, а другие не менее именитые программисты могут считать, что лучше использовать деление с округлением к нулю или даже евклидово деление.

Поэтому просто запомните, что в Python при делении с остатком результат округляется в меньшую сторону, а не к нулю, и что остаток всегда имеет тот же знак, что и делитель.